0. UnderSampling
언더샘플링(Under Sampling)은 오버샘플링(Over Sampling)과 반대되는 개념으로, 데이터 간 불균형을 해소하기 위한 기법 중 하나이다.
소수 클래스(Minority Class)의 데이터 양을 다수 클래스(Majority Class)에 맞춰 증가시키는 것이 오버 샘플링이라면, 다수 클래스의 데이터 양을 감소시키는 것이 언더샘플링이라고 할 수 있다.
0.1. Sample Dataset
import pandas as pd
import numpy as np
from sklearn.datasets import make_classification
import seaborn as sns
import matplotlib.pyplot as plt
random_seed = 43
X,y = make_classification(n_samples = 300, n_features = 2, n_informative = 2, n_classes = 3,
n_redundant = 0, n_clusters_per_class = 1, weights = [0.2, 0.3, 0.5],
random_state = random_seed)실험을 위해 임의의 데이터셋을 생성하였다.
샘플은 총 300개이며 [0, 1, 2] 세 개의 클래스 중 하나의 클래스에 속한다. 각 샘플은 2차원의 특징(feature)을 가진다.
각 클래스별 샘플 개수는 동일하지 않으며, [0.2, 0.3, 0.5]의 비율을 나눠가진다. (각 클래스별 샘플 개수는 [63, 91, 146]이다.)
0.2. Sampler Class
class Sampler():
def __init__(self, X,y):
self.X = X
self.y = y
self.X_resampled = None
self.y_resampled = None
self.resampler = None
self.df = None
self.df_resampled = None
self.df_no_dups = None
def set_sampler(self, sampler):
self.resampler = sampler
def resample(self):
self.X_resampled, self.y_resampled = self.resampler.fit_resample(self.X, self.y)
self.counter()
self.to_dataframe()
self.compare()
def counter(self):
counter = [0]*3
for y in self.y_resampled:
counter[y] += 1
print(counter)
def to_dataframe(self):
self.df = pd.DataFrame(self.X, columns = ['x0', 'x1'])
self.df['y'] = self.y
self.df['original'] = [1] * len(self.df)
self.df_resampled = pd.DataFrame(self.X_resampled, columns = ['x0', 'x1'])
self.df_resampled['y'] = self.y_resampled
self.df_resampled['original'] = [0] * len(self.df_resampled)
self.df_no_dups = pd.concat([self.df, self.df_resampled]).drop_duplicates(subset = ['x0', 'x1'], keep = False)
self.df_no_dups['original'] = [2] * len(self.df_no_dups)
def compare(self):
df_total = pd.concat([self.df, self.df_resampled, self.df_no_dups])
sns.relplot(data = df_total, x = df_total.x0, y = df_total.x1, hue = df_total.y, col = df_total['original'])
plt.show()
sampler = Sampler(X, y)편의를 위해 Sampler 클래스를 제작하여 사용하였다.
Sampler instance는 sklearn.under_sampling 내의 인스턴스를 받아 원본과 언더샘플링 이후의 결과값을 비교하는 데 사용한다.
1. Cluster Centroid
from imblearn.under_sampling import ClusterCentroids
cc = ClusterCentroids(random_state = random_seed)
sampler.set_sampler(cc)
sampler.resample()
# [63, 63, 63]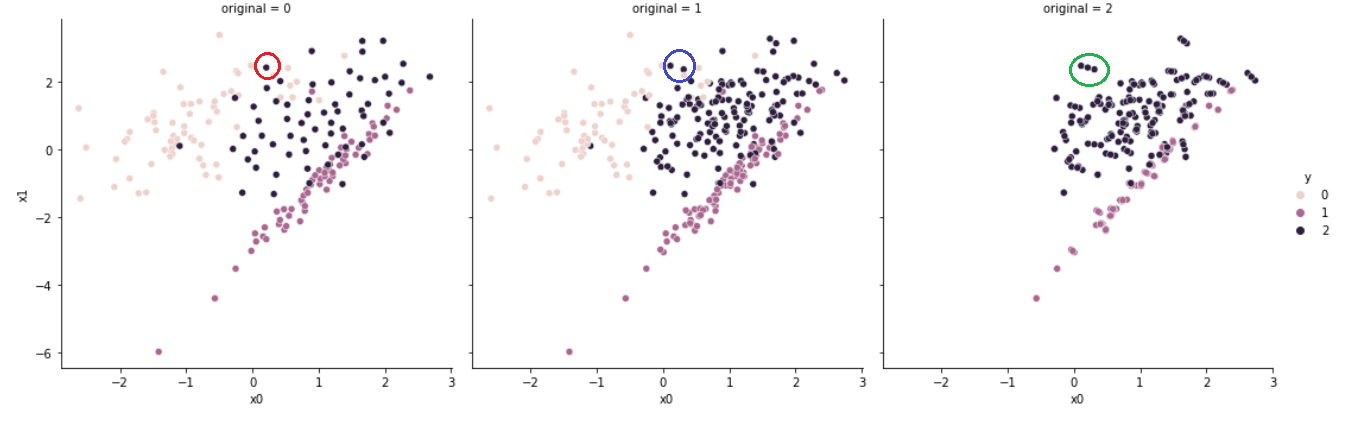
세 개의 그래프 중 왼쪽 그래프(original = 0)는 Under Sampling 후의 결과이며, 가운데 그래프(original = 1)는 원본 데이터, 오른쪽 그래프(original = 2)는 원본과 샘플링한 데이터 간 차이를 나타낸다.
Cluster Centroid는 K-means 알고리즘을 사용한다.
원본 데이터가 생성하는 군집의 중심(Cluster Centroid)을 기준으로 하여, 군집의 중심을 유지할 수 있는 새로운 데이터를 생성(generate)한다.
따라서 샘플링 후의 데이터는 원본 데이터와 상이할 수 있다.
이는 원으로 표시한 부분을 보면 쉽게 확인할 수 있는데, 붉은 원으로 표현된 데이터는 새로이 생성된 데이터이며, 파란 원으로 표현된 데이터는 제거된 데이터이다. 이러한 변동이 있었다는 것을 초록색 원으로 표현된 데이터를 통해 확인할 수 있다.
2. Random Under Sampler
from imblearn.under_sampling import RandomUnderSampler
rus = RandomUnderSampler(random_state = random_seed)
sampler.set_sampler(rus)
sampler.resample()
# [63, 63, 63]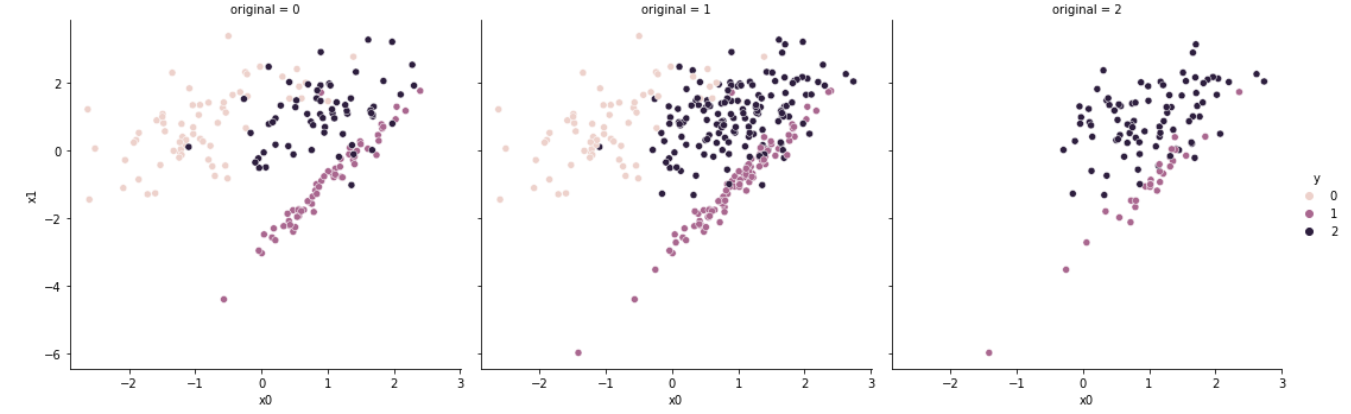
Random Under Sampler는 가장 직관적인 방법으로 언더샘플링을 수행한다. 다수 클래스 샘플 중 무작위의 샘플을 선택하여 제거하여, 최종적으로 소수 클래스와 샘플 개수를 맞춘다.
이후 방법론들은 다수 클래스 중 샘플을 선택(select)한다는 점에서 데이터를 생성하는 Cluster Centroid와 차이를 가진다.
3. Near Miss
from imblearn.under_sampling import NearMiss
nm = NearMiss(version = 1)
sampler.set_sampler(nm)
sampler.resample()Near Miss는 Nearest Neighbours 알고리즘을 사용하며, 클래스는 version 파라미터를 기준으로 세 가지 다른 방법론을 적용한다.
3.1. NearMiss-1
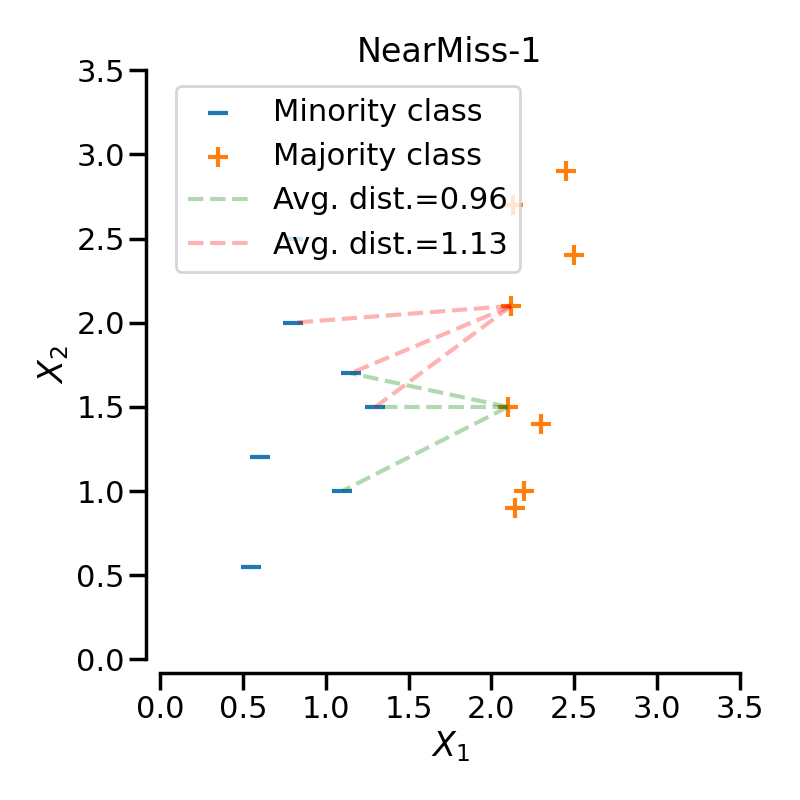
version = 1로 설정하면 소수 클래스와 가장 가까운 다수 클래스의 데이터를 남긴다.
즉, 특정 다수 클래스 샘플로부터 가장 가까운 $N$ 개의 소수 클래스 샘플까지의 평균 거리를 구한다. 이후, 평균 거리가 가장 가까운 $M$ 개의 데이터를 선택하여 남기고, 나머지 샘플을 제거한다.
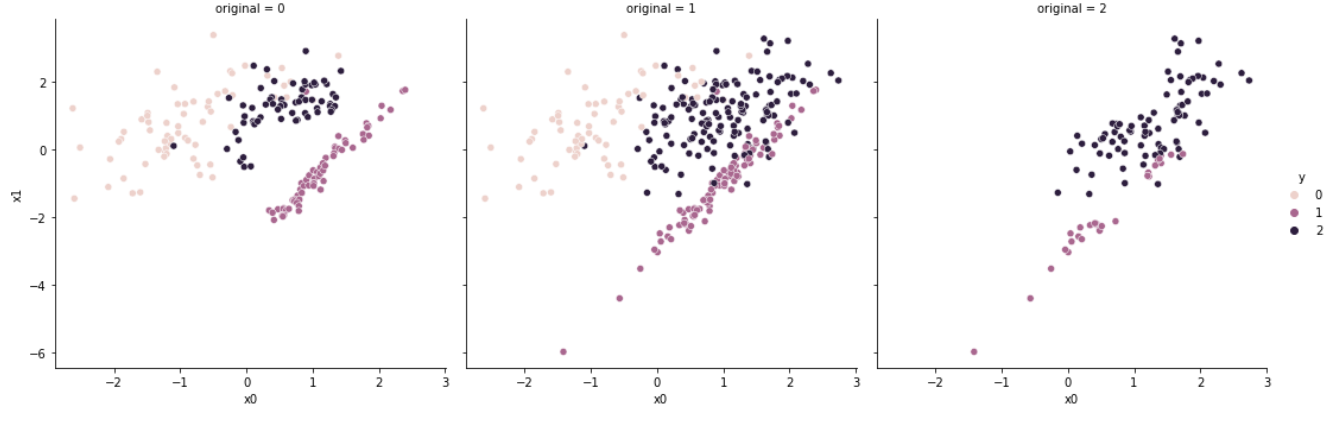
결과적으로 밝은 살구색으로 표현된 소수 클래스(y = 0)로부터 거리가 가까운 샘플만이 남아있음을 확인할 수 있다.
일반적으로는 클래스 사이의 경계선에 샘플이 생성되지만, 특정 샘플이 다른 클래스의 경계를 침범하여 존재한다면, 해당 샘플 근처의 데이터만 선택되어 노이즈(Noise)에 취약하다는 단점이 있다.
3.2. NearMiss-2
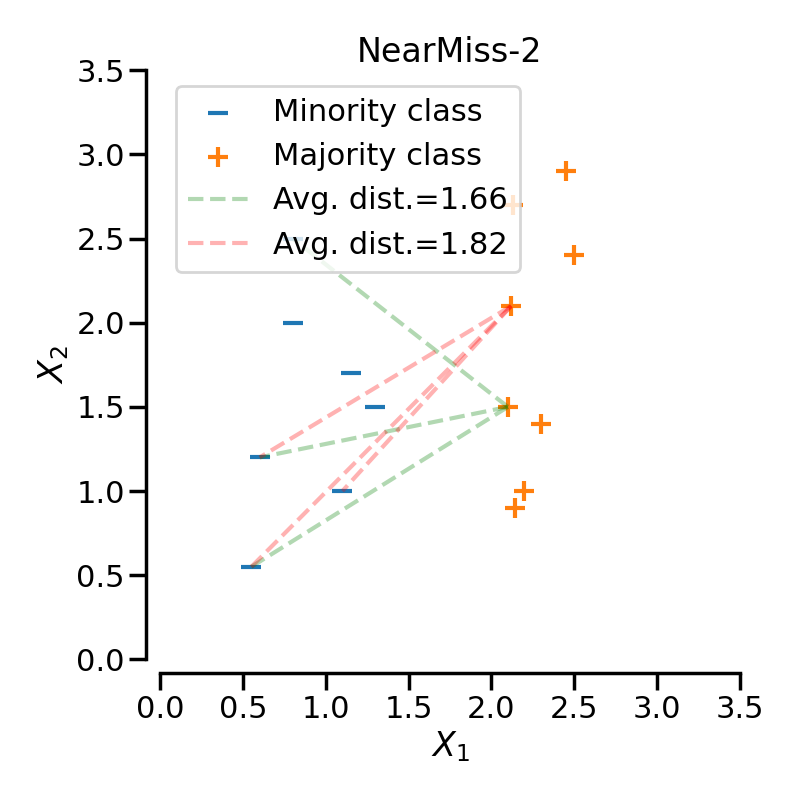
특정 다수 클래스 샘플로부터 가장 먼 $N$ 개의 소수 클래스 샘플까지의 평균 거리를 구한다. 이후, 평균 거리가 가장 가까운 $M$ 개의 데이터를 선택하여 남기고, 나머지 샘플을 제거한다.
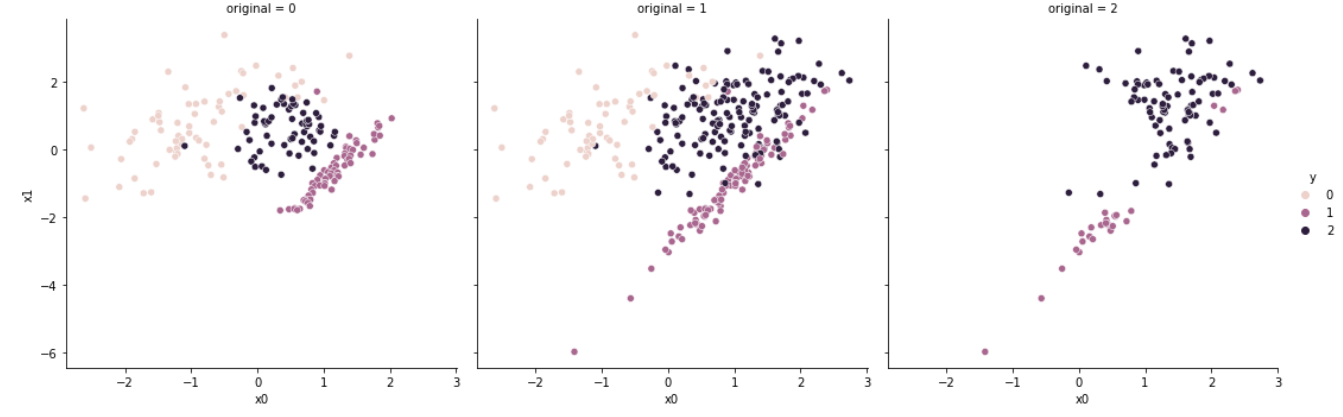
NearMiss-1과 NearMiss-2는 소수 샘플로부터 가까운 데이터를 선택한다는 공통점이 있다. 그러나 NearMiss-2는 가장 먼 소수 샘플까지의 거리를 계산한다는 차이점을 가진다.
NearMiss-1과 마찬가지로 가장 먼 거리에 존재하는 marginal outlier의 존재가 균등한 샘플링을 방해할 수 있다.
3.3. NearMiss-3
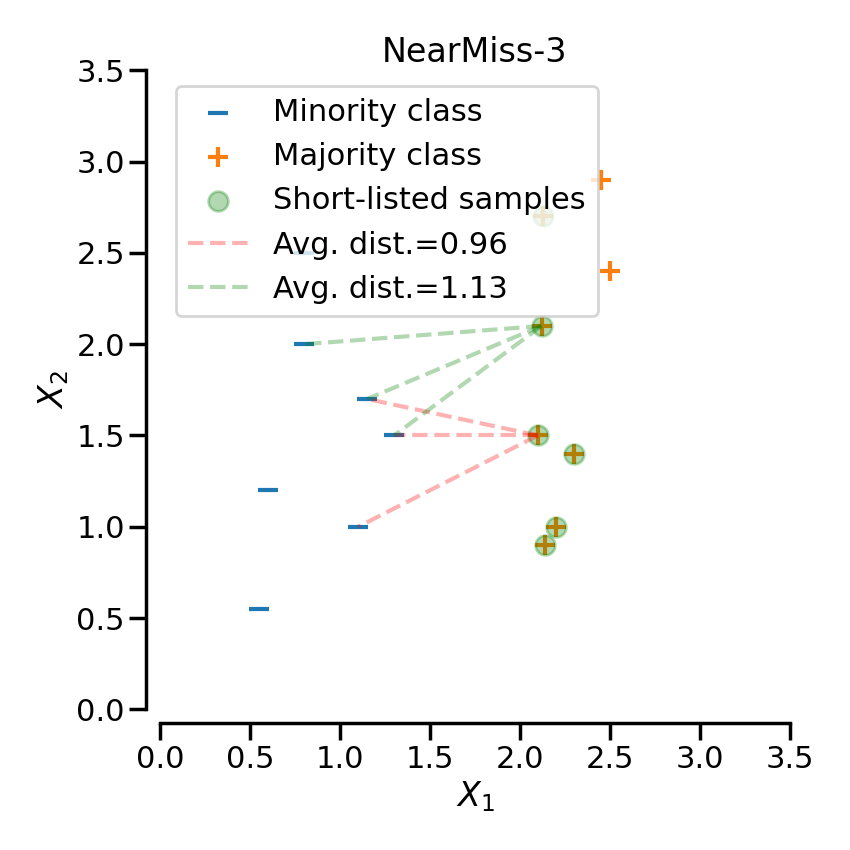
NearMiss-3은 모든 소수 클래스 샘플로부터 $M$ 개의 가장 가까운 다수 클래스 샘플을 보존(kept)한다. 보존된 다수 클래스 샘플로부터 $N$ 개의 가장 가까운 소수 클래스 샘플까지의 거리를 계산하여, 평균 거리가 가장 먼 샘플을 선택한다.
가장 가까운 거리의 샘플과 가장 먼 거리의 샘플을 모두 고려하기 때문에 세 가지의 방법론 중 Noise에 가장 강건(Robust)하다.
4. Tomek Links
from imblearn.under_sampling import TomekLinks
tomek = TomekLinks()
sampler.set_sampler(tomek)
sampler.resample()
# [63, 80, 126]TomekLinks 클래스는 Tomek Link를 형성하는 샘플을 제거한다.
세 개의 샘플 $x_{1}, x_{2}, x_{z}$가 존재한다고 가정해보자. $x_{i}$는 샘플 $x$가 $i$ 클래스에 속해있음을 나타내며, $x_{z}$는 임의의(any) 샘플을 나타낸다.
$d(x_{1}, x_{2}) < d(x_{1}, x_{z})\ and\ d(x_{1}, x_{2}) < d(x_{2}, x_{z})$일 때, $x_{1}$와 $x_{2}$ 사이에는 Tomek Links가 있다고 말할 수 있다.
다시 말해, 서로 다른 클래스에 속한 두 개의 샘플이 서로에게 가장 가까운 샘플일 때 Tomek Links를 생성한다고 할 수 있다.
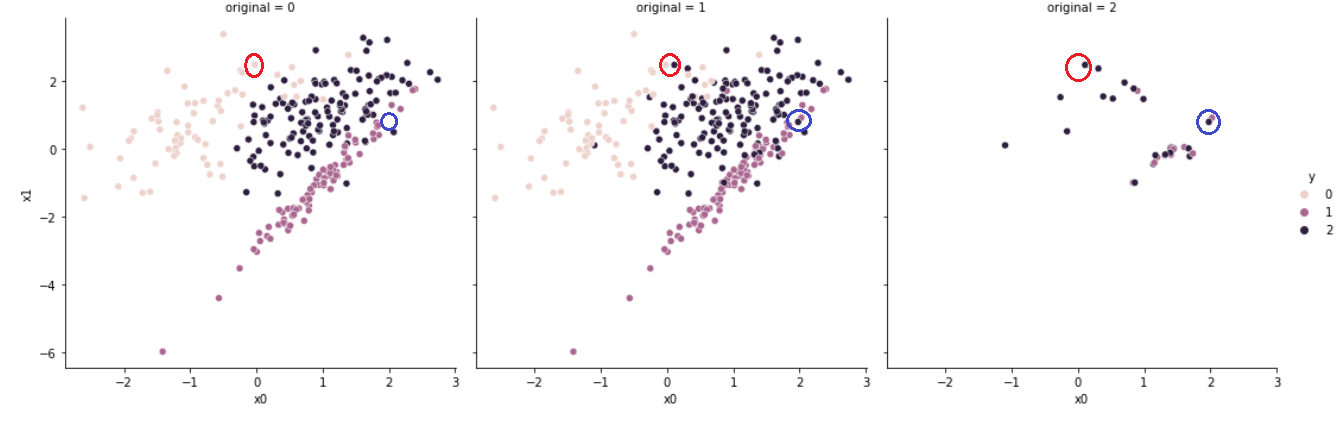
붉은 원을 보면 살구색의 데이터와 남색의 데이터가 서로에게 가장 가까운 존재이기에 남색의 데이터가 제거되었음을 확인할 수 있다. 살구색의 데이터가 사라지지 않은 이유는 해당 데이터가 소수 클래스에 속해있기 때문이다.
파란 원을 보면 남색의 데이터와 보라색의 데이터가 서로에게 가장 가까운 존재이기에 두 데이터가 모두 제거되었음을 확인할 수 있다.
Tomek Links를 생성하는 데이터 중, 어떤 데이터를 제거할지는 sampling_strategy parameter를 통해 결정할 수 있으며, 기본값(default = auto)는 소수 클래스를 제거하지 않는다.
5. Edited Nearest Neighbours
from imblearn.under_sampling import EditedNearestNeighbours
enn = EditedNearestNeighbours()
sampler.set_sampler(nm)
sampler.resample()
# [63, 63, 63]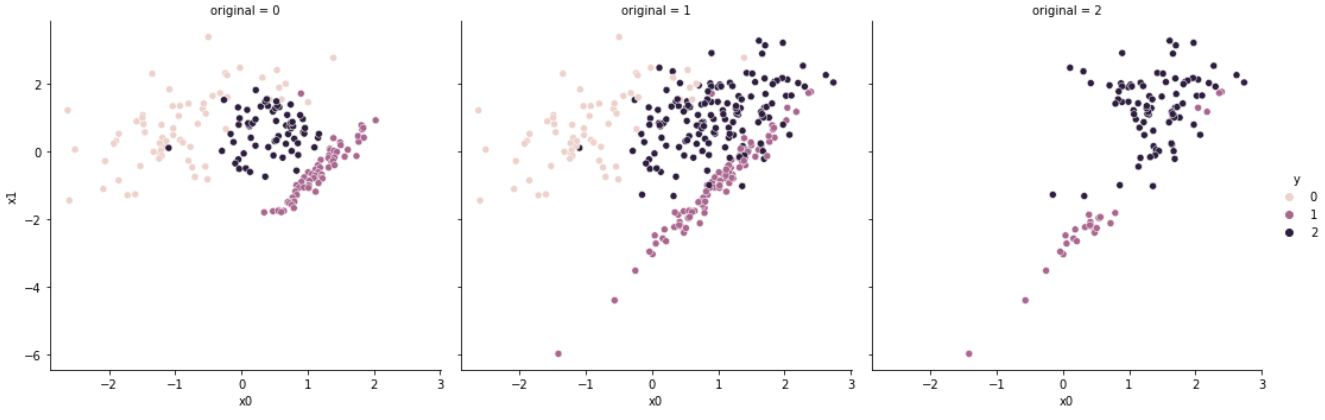
Edited Nearest Neighbours는 K-nearest Neighbours 알고리즘을 통해 언더샘플링을 수행한다.
특정 데이터 샘플 $x_{i}$를 기준으로 KNN을 실시하여, (i) $K$개의 샘플이 모두 $i$ 클래스에 속하거나(kind_sel = 'all'), (ii) $K$개의 샘플 중 다수가 $i$ 클래스에 속하는 경우(kind_sel = 'mode')가 아니면 해당 샘플을 삭제한다.
5.1 RENN, AllKNN
RENN(Repeated Edited Nearest Neighbours)와 AllKNN은 앞서 언급한 ENN을 변형한 알고리즘이다.
RENN은 데이터 리샘플링의 결과가 바뀌지 않을 때까지 ENN을 반복적으로 실시하는 것이며, AllKNN은 $K$의 값을 점차 증가시켜가면서 ENN을 반복적으로 실시하는 것이다.
앞서 NearMiss-1이 클래스가 다른 가장 가까운 데이터들을 남겨두는 것으로 경계선 주위에 데이터를 형성하였다면, ENN 계열은 경계선 주위의 데이터를 제거한다.
6. Condensed Nearest Neighbour
from imblearn.under_sampling import CondensedNearestNeighbour
cnn = CondensedNearestNeighbour()
sampler.set_sampler(cnn)
sampler.resample()
# [63, 5, 25]CNN은 1-Nearest Neighbours 알고리즘을 사용하며, 알고리즘의 진행 순서는 다음과 같다.
- 모든 소수 클래스 샘플을 집합 $C$로 둔다.
- 다수 클래스(Targeted Class)의 샘플 하나를 집합 $C$에 포함하며, 나머지 샘플들은 집합 $S$로 둔다.
- 집합 $S$ 내의 모든 샘플에 대하여, 1-NN을 실시한다.
- 오분류(misclassfied)된 샘플에 대하여 집합 $C$에 추가한다.
- 집합 $C$에 변화가 없을 때까지 3-4번 과정을 반복한다.
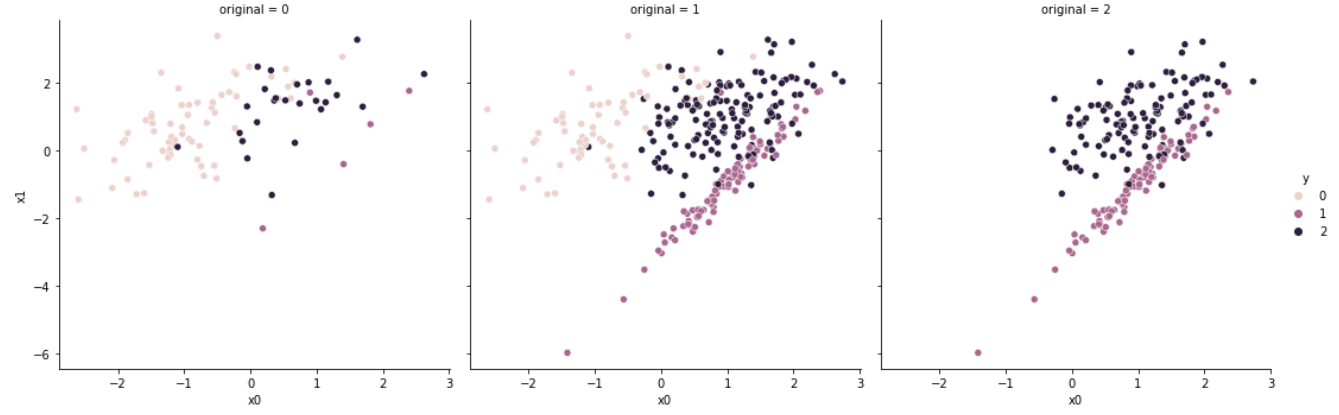
즉, 다수 클래스에 속한 샘플 중, 소수 클래스와 가장 가까운 데이터만을 남기는 것으로 경계면을 학습하는 것이다.
6.1. One-sided Selection
from imblearn.under_sampling import OneSidedSelection
oss = OneSidedSelection()
sampler.set_sampler(oss)
sampler.resample()
#[63, 28, 84]OSS는 Tomek Links를 적용하여 resample된 데이터셋에 CNN을 적용하는 것이다.
Tomek Links는 경계면에 있는 데이터를 제거하며, CNN은 경계면에 있지 않은 데이터를 제거하기에 두 방법론의 단점을 상호 보완해준다.
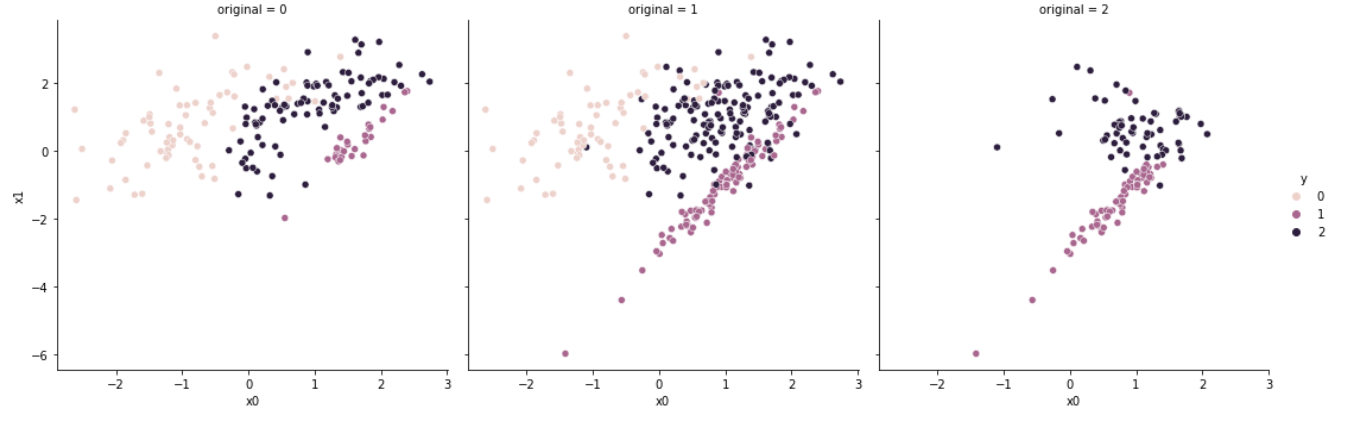
7. Instance Hardness Threshold
from sklearn.linear_model import LogisticRegression
from imblearn.under_sampling import InstanceHardnessThreshold
iht = InstanceHardnessThreshold(random_state=random_seed,
estimator=LogisticRegression(solver='lbfgs', multi_class='auto'))
sampler.set_sampler(iht)
sampler.resample()
#[63, 63, 63]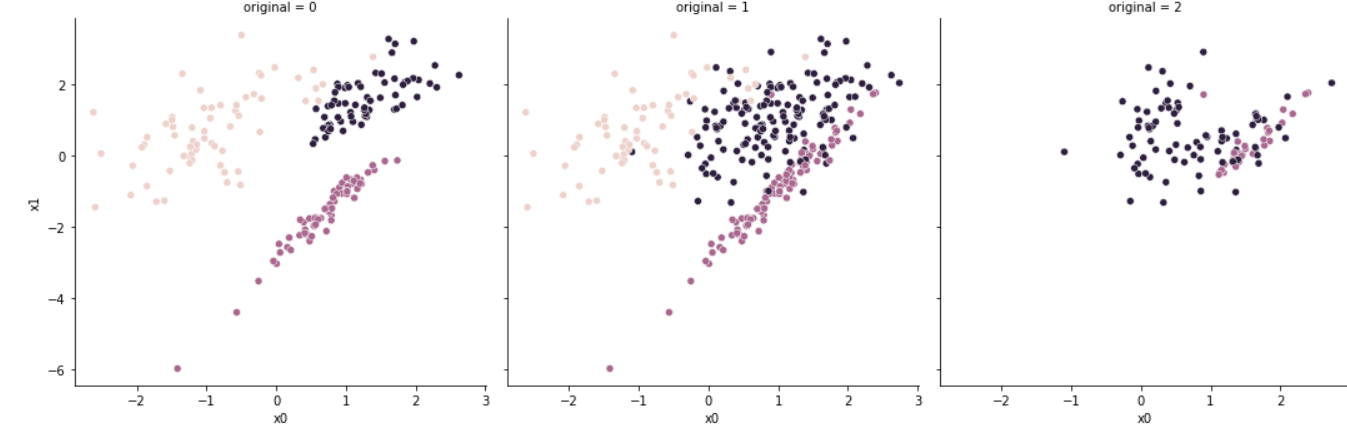
Instance Hardness Threshold는 estimator라는 parameter를 필요로 한다.
estimator는 데이터를 바탕으로 cross validation을 통해 학습을 하며, 특정 데이터가 어느 클래스에 속할지 확률값을 계산한다.
이후, 다수 클래스 내 샘플 중, 해당 클래스에 속할 확률이 가장 적은 데이터를 제거하는 것으로 언더샘플링을 진행한다.
8. 참조
'개인 공부 > DS' 카테고리의 다른 글
| [DS] MCMC (Monte Carlo Markov Chain) (0) | 2023.07.17 |
|---|---|
| [DS] 수요 예측 (0) | 2023.07.16 |
| [DS] 베이시언 결정 이론 (0) | 2022.12.23 |
| [DS] Over Sampling (RandomOverSampler, SMOTE, ADASYN) (0) | 2022.12.23 |
| [DS] PCA 차원 감소 (PCA Dimensionality Reduction) (0) | 2022.12.23 |